Рак анального канала — это относительно редкая форма рака, которая возникает в анальном канале,
В мире профессиональной видеосъемки, качество изображения и точность контроля над кадром имеют решающее значение.
Первая стадия алкоголизма часто проходит незамеченной, поскольку признаки и симптомы могут быть тонкими и
Юридические услуги играют ключевую роль в обеспечении правовой поддержки как для индивидуальных лиц, так
Кодирование от алкоголизма сегодня является одним из самых распространенных и эффективных методов борьбы с
Предоставление больничного листа работодателю - это важная процедура, которая требует внимательности и точности.
Одним из способов создать положительную атмосферу в косметологическом кабинете является приобретение качественной и красивой
Красная рыба, благодаря своему богатому вкусу и пользе для здоровья, является популярным выбором для
Steam аккаунты служат входными воротами в мир цифровой дистрибуции игр и программного обеспечения, предоставляемого
Абдоминальный хирург - это специалист, который занимается диагностикой и лечением заболеваний, связанных с органами
Реабилитация не ограничивается лишь медицинской помощью; она включает в себя целый комплекс мер, направленных
Пластиковые емкости большого объема, такие как бочка 10000 литров, играют важную роль в различных
Комплексное обследование организма – это фундаментальная составляющая современной медицинской практики, позволяющая получить полное представление
Аппаратный вакуумно-роликовый массаж — это современная косметологическая процедура, которая сочетает в себе преимущества вакуумного
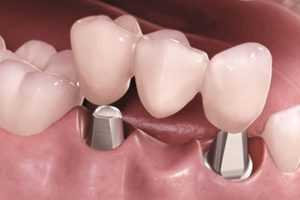
Стоматологическая клиника - это место, где пациенты обращаются за помощью в решении различных проблем
Современная кухня – это не только место приготовления пищи, но и сердце дома, где
В процессе массажа используются различные техники растирания, разминания и поглаживания, которые способствуют улучшению кровообращения
Выбор каминной топки зависит от многих факторов, включая размер помещения, стиль интерьера и личные
Аптечка КИМГЗ (Комплект Изделий Медицинского Назначения Гражданской Защиты) — это основной элемент системы оказания
Цветочные мотивы в одежде не только придают образу свежесть и оригинальность, но и помогают
Антивозрастная медицина играет важную роль в обществе, поскольку способствует увеличению продолжительности активной и здоровой
Вывод из запоя – это комплексная медицинская процедура, направленная на оказание помощи людям, страдающим
Терапевтические группы представляют собой форму психотерапии, где лечение происходит в групповом формате под руководством
В современном мире цифрового маркетинга, накрутка подписчиков в Telegram стала одним из ключевых инструментов
Современные технологии, такие как 3D-печать и компьютерное моделирование, революционизировали процесс изготовления зубных протезов.
О пользе силового спорта для представительниц слабого пола - приводятся доводы в пользу регулярных
Наркология является важной областью медицинской науки, занимающейся изучением, диагностикой и лечением зависимостей различного происхождения.
Замороженная стручковая фасоль является одним из наиболее популярных и удобных вариантов здорового питания.
Главная особенность выездного кейтеринга заключается в его мобильности и гибкости: специалисты компании берут на
Антистресс-таблетки стали популярным средством для облегчения психологического дискомфорта и улучшения общего самочувствия.